|
Mars Telecommunications Orbiter:
MTO Would Have Extended the Internet to Mars
NASA had planned to extend the Internet to Mars with the launch of the Mars Telecommunications Orbiter (MTO) in 2009.
A NASA JPL artist imagines a laser beam from the Mars Telecommunications Orbiter carrying science data from the Red Planet to Earth as an interplanetary extension of the Internet. CLICK IMAGE TO ENLARGE
The MTO spacecraft would have arrived in a high orbit above Mars in 2010 and then would have been used to relay Internet-style data packets to Earth from a variety of Mars landers and orbiters for as much as ten years.
Sooner or later, such a dedicated communications satellite will be necessary due to the vast quantity of science information to be sent to Earth by such landers as the roving Mars Science Laboratory of 2009.
Unfortunately... On July 21, 2005, NASA announced cancellation of MTO because the space agency needed to support a Hubble servicing mission, the Mars Exploration Rover extended mission operations, and the Mars Science Laboratory to fly in 2009. The cancellation also saved Glory, an Earth science mission.
The space agency will launch the Mars Science Laboratory in 2009.
The Moon. NASA would like to send a similar interplanetary Internet hub to the Moon because there are lots of missions to lunar orbit and the lunar surface planned by Japan, India, China, Europe and the United States.
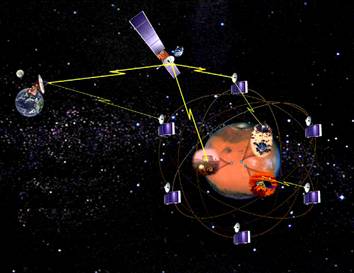
What might have been. MTO would have arrived in a high orbit over Mars in 2010. From there, it would have served as an Internet hub, receiving a flood of science information as data packets from a growing fleet of Mars probes, orbiters, landers, rovers and science stations, and relaying them to Earth for as much as ten years.
The interplanetary Internet would have linked disparate science missions such as Mars Global Surveyor, Mars Odyssey, Europe's Mars Express Orbiter, Mars Reconnaissance Orbiter, and the future Phoenix Mars Scout and Mars Science Laboratory landers.
Data rate. MTO not only would have been able to send data to Earth via high-speed X-band and Ka-band radio signals, but also via laser light beams. That was expected to bring a tenfold increase in bandwidth Ð the rate of data transmission.
That data transmission speed had been likened to four "T1 lines" that might be found in use on Earth.
Three CDs a day. Orbiting 3,000 miles above the Red Planet, MTO would have been in contact with Earth around the clock. That high orbit would have been 20 times farther from the planet surface than other orbiters. From up there, it would have had a direct line of sight to Earth.
Laser beam. While the optical communication signals arriving at Earth would have been susceptible to blocking by clouds, they would have been able to carry 10,000 times more data than microwave radio signals. MTO would have been able to transmit the equivalent of three compact disks of data each day.
MTO firsts. Mars Telecommunications Orbiter would have been that planet's first high-speed data connection and the first interplanetary spacecraft dedicated to providing communications services to other spacecraft.
The spacecraft would have orbited the Red Planet at a higher altitude than most other orbiters so it could have provided effective relay of science data from surface missions on the ground such as the roving Mars Science Laboratory.
MTO would have communicated with Earth on two radio wavelength bands and also by an optical laser communicator.
Internet hub. MTO will be the hub of a growing interplanetary Internet on Mars.
A NASA JPL artist imagines a group of satellites around Mars providing navigation and communication for robots and humans down on the Red Planet, while a larger spacecraft ensures the Mars-Earth connection. CLICK IMAGE TO ENLARGE
It would have linked NASA's orbiting spacecraft Mars Global Surveyor, Mars Odyssey and Mars Reconnaissance Orbiter, Europe¹s Mars Express Orbiter, Mars Phoenix Lander, and the Mars Science Laboratory on the surface.
Future landers, rovers, science stations, and orbiting spacecraft all would have communicated with each other and with Earth by sending and receiving signals via MTO.
NASA had planned to land the Mars Science Laboratory a month after the Mars Telecommunications Orbiter would have entered orbit above the planet. The lab is designed to send out a robot rover to make detailed scientific observations of the martian surface.
High in the martian sky. MTO would have orbited the Red Planet at an altitude of about 3,000 miles. That's 20 times farther from the planet's surface than other spacecraft. From up there, MTO almost always would have had a direct line of sight to Earth so it could be in contact with the home planet nearly around the clock.
Laser beam. In addition to communicating at radio frequencies, the Mars Telecommunications Orbiter would have used a laser beam for planet-to-planet communications.
The lasers would transmit and receive signals using near-infrared light. That's just beyond the portion of the electromagnetic spectrum seen by the human eye.
While such optical communications signals are more susceptible to interference from clouds, they can transmit 10,000 times more data than microwave communications.
A whole lot of data. MTO would have relayed the equivalent of three full compact disks of data to Earth each day during its 10-year working life.
Tiny companion. Mars Telecommunications Orbiter also would have released a small satellite – a sphere the size of a soccer ball. MTO would have tracked that device as it orbited Mars.
The robot Mars Sample Return mission in 2013 would collect and bring Mars rocks back to Earth. Successful retrieval of those samples would depend on such an orbiting spacecraft to accurately track and intercept the sample container launched from the martian surface. MTO's tracking of its small satellite would have demonstrated such a capability.